You've heard that a portrait lens is the one with a focal length of 50mm or above and that wide angle lenses create a distorted image when used for portraits. This article will try to help you understand and overcome that prejudice.
What Is a Portrait?
Portraits of people can be all kinds of images, from the paintings of the masters of old to the masters of photography today. It's an image of a person fit in a frame of a certain geometry. The portrait is not just the head of the person. There's a special term in photography for that: a headshot. A portrait can be a full-body image too.
'Wide Angle Lenses Distort the Face,' They Say
This is where the misconception comes. In theory, a wide angle lens should capture more of the view in front of the camera than a longer lens, which means it will change to a certain extent the viewing perspective from what we see with our own eyes. Objects that are close to each other will look farther apart with a wide angle lens. It will also have different depth-of-field properties per aperture: wide angle lenses have a deeper depth of field than longer focal lengths at the same aperture. For this reason, the blur of the background and the foreground (assuming the subject is in the mid-ground) is more prominent with longer lenses.
"OK, but wide lenses distort the image. This is why they are not liked for portraits; it's not the depth of field or what they see." This is the common complaint.
Why Is There Distortion With Wide Angle Lenses?
If you have shot with a wide angle cinema lens, it will change your mind about what you call "distortion." The optical defect that makes most photographers avoid using wide angle lenses is a radial-looking distortion that is different from the perspective distortion of the lens. The radial distortion is making the image look as if areas closer to the periphery of the lens are bent inwards or outwards.
To illustrate that in a different way, let's suppose we have a wall, which we look at from the side with a 50mm lens on a full-frame sensor (a) and with a wide angle lens on the same sensor. A wide angle lens without radial distortion (b) will change the perspective, as you see in the middle, while a radial distortion defect (c) will bend the lines that are closer to the periphery of the frame, and thus, you will no longer have straight lines in these areas.
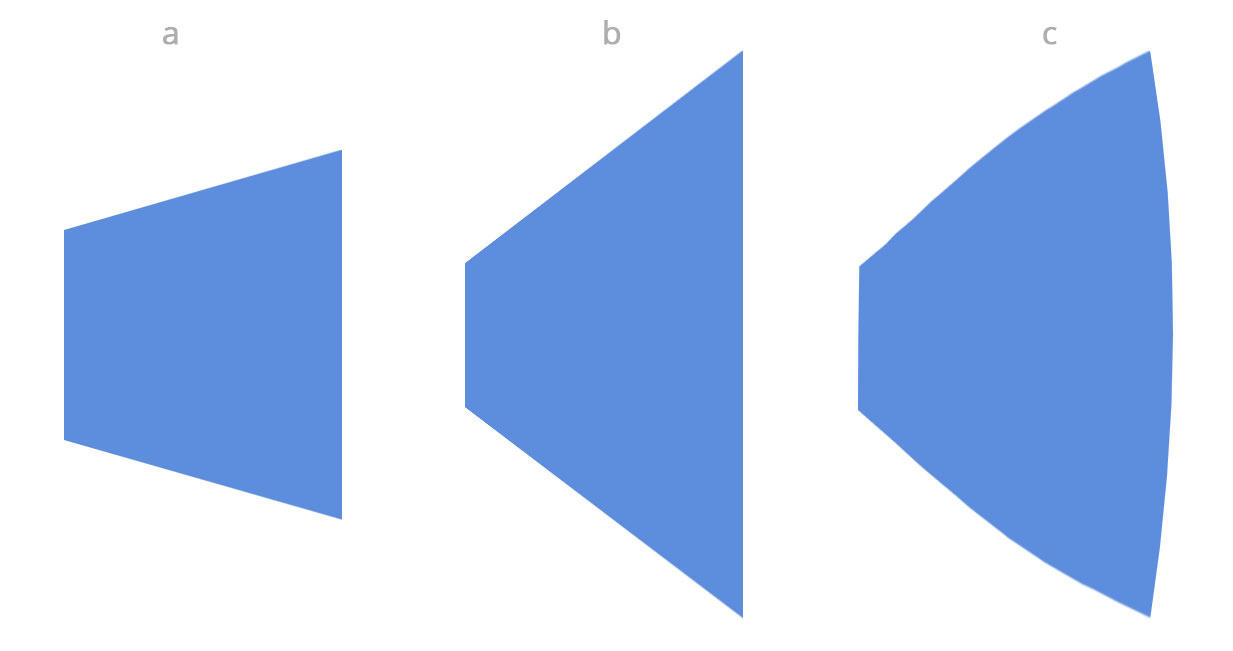
There's a radial distortion with longer lenses too, but few people complain about it. That defect is not supposed to be there. As making a lens without or with a minimal radial distortion is an expensive process, most manufacturers decide to leave it, and today it's used for artistic purposes. If you purchase a quality wide angle cinema lens, the radial distortion there is very small if not almost eliminated. If you take the radial distortion seriously and correct it with any lens, you use your will start loving the different perspective of the wide angle view without the lines bending and will start to incorporate that look more and more in your images.
In the following video, you will find tests with different 14 mm cinema lenses and the radial distortion (called simply "distortion" in the video) will be close to none. You may be surprised how a wide angle view should normally look compared to what most still lenses do today.
https://www.youtube.com/watch?v=ZHIWHCU2Z30
How to Deal With Wide Angle Lenses' Radial Distortion?
The obvious remedy is to buy lenses with almost-eliminated radial distortion, but if you can't afford them, learn how much your lens is distorting the image, as it's different from lens to lens. There are two methods, which work best if they are both applied: compose accordingly and fix the rest in post.
Important Things Should Be Away From the Edges
In most cases, wide angle lenses tend to deform the areas close to the borders of the frame. If you have objects there, whether these are human faces, limbs, or rear parts of the body, they will look bigger than normal. To avoid that, keep important objects away from the edges of the frame, also because you may need to crop these areas out in post.
Fix It in Post
You can either crop out the border regions or try to correct some of the distortion to an extent that it's bearable, which will inevitably make you crop some of the pixels out.
Use a Camera With More Resolution
If the image is heavily distorted, you can crop out some of it and leave the normal-looking part without losing much of the resolution that is usually used today.
Conclusion
Avoiding wide angle lenses is avoiding the defects they are built with. Knowing how to use them will help you take advantage of the environment you see with your own eyes. Including more of the environment tells a different story and lets the viewer's eyes wander around, enjoying the details, especially if they are masterfully presented.
Up until recently I never would have considered using a wide angle lens for portraits, but I really like the results I have gotten with mine. It certain situations it can work wonders.
Yes, indeed. The perspective is unique especially if the image doesn't look crooked, but simply "different."
Because people read and stick to rules too much instead of shooting.
The same with shooting landscapes with long lenses.
Why are [INSERT THING HERE] misunderstood and avoided for [INSERT PURPOSE HERE]
Because people who beginners look up to, misuse terms, say things which are incorrect, oversimplify, and leads them to misunderstandings and fear.
Here a few of these things, in this article alone.
PERSPECTIVE
«…a wide angle lens… than a longer lens,… will change to a certain extent the viewing perspective….»
Perspective is simply a matter of where we stand relative to the subject. It is not in anyway* dependent on the lens, nor the sensor size. *Unless one insists that a certain lens or sensor size “makes” them come in closer or stand further back, thus a correlation. But the effective change in perspective is achieved by the position in space, not the lens on the camera. If three photographers stood at the same spot with three different lenses and cameras, they would all get the same perspective.
«Objects that are close to each other will look farther apart with a wide angle lens.»
Again, the perspective is not from the lens, but from the relative distances between the objects and the camera. It does not matter what lens is used, if the photographer is in the same spot, and/or the relative object-camera distances are the same, the objects will NOT look any closer, nor further apart.
APERTURE and DoF
«…wide angle lenses have a deeper depth of field than longer focal lengths at the same aperture.»
Many photographic teachers keep using the term Aperture and f-Number interchangeably, They are not. Aperture is the diameter of the iris, measured in millimetres, and f-Number, ‘N’, is the focal ratio, which is the ratio of the focal length, ‘f’, to the aperture, ‘D’. and has no dimensions. It is given by,
N=f/D
therefore,
D=f/N
which is why Aperture is stated as f/2.8, f/3.5, f/4, f/5.6, etc. The aperture is the diameter, not the f-number, N, stated as 2.8, 3.5, 4.0, 5.6, etc.
That being said, the DoF decreases with aperture, (and is the same for any given aperture on any lens), and the amount of light entering the box decreases with f-Number. Any lens with f-number 4.0 will let in the same amount of light, but any lens with an aperture of 25mm will have the same DoF. To wit, a 50mm @ f/2.0, a 100mm @ f/4.0, and a 200mm @ f/8.0 will all have a 25mm aperture, and give the same DoF, but will require adjustments in either Lv, Tv, Sv, or EI to compensate for exposure.
BARREL/PIN CUSHION DISTORTION
«The radial distortion is making the image look as if areas closer to the periphery of the lens are bent inwards [pin-cushion] or outwards [barrel].»
You have actually got this correct. Radial distortion can and does happen on less expensive lenses, regardless of the focal length, and, whereas many people think that wide-angle lenses tend to barrel, [your (c) illustration], and telephoto lens tend to pin-cushion, this is not always the case, and one can see pin-cushion distortion on a wide lens, just as easily as they can see barrel distortion on a long lens.
What you got wrong was the illustrations (a) and (b). The difference seen here will only happen if the photographer got closer to the wall with the wide-angle lens. If he stayed at the same distance, he would have seen the same wall, just smaller.
«…wide angle lenses tend to deform the areas close to the borders,… they will look bigger than normal.»
In your defence, you did say, “In most cases.” I have not done any sampling to see if that is true, but I can say that, in some cases, they will look smaller than normal. To be more precise, when there is barrel distortion, the edges will look bigger, and the corners will look smaller. When there is pin-cushion distortion, the corners will look bigger and the edges will look smaller.
CROP THE EDGES
When one does radial distortion correction in processing, —or any kind of geometric distortion corrections— it will result in the need to crop out the dark areas which are left behind, (or fill them somehow). What one needs to also add to this is that cropping will always give the effect of using a lens of a more narrow FoV, as cropping narrows the FoV. That may seem kind of obvious, but when it comes to teaching beginners, we need to not assume that things are obvious.
FINAL REMARK
«Avoiding [INSERT THING HERE] is avoiding the defects they are built with.»
That is only with those things which have defects, —which, arguably, is everything— instead of looking for the things without obvious defects, like better lenses. Most lens reviews discus how much radial distortion is noticeable in the image, and, just like lenses with heavy diffraction, bright internal reflections, copious chromatic aberrations, etc., are to be avoided, so are [any] lenses with plenty of radial distortion.
However, the best lens is the one you have, so one must learn how to cope with the issues at hand, whatever they may be.
Can you put this in clif notes?
When photographers shoot from the same place they all will see the same objects regardless of the lens, but the wider lenses (without the radial distortion) will change the perception of distances between objects. It will not see what's behind that corner or something else, but the way the objects are projected onto the sensor is different than with other focal distances. There are 2 distortions: the normal change of objects relation perception and the defects that are introduces such as the radial distortion (like a barrel distortion). When we eliminate the radial one we are left with the other "distortion" which changes the perceptions of distances between objects like the further away objects seemingly look further away than they are in relation to closer objects.
One can't avoid the perspective perception change with a wider lens even without the radial distortion, because it's simply physics. The standard known formula for a magnification glass is 1/image + 1/object = 1/focal_length, where "object" is the distance from the object to the lens and "image" is the distance of the object to the image (an imaginary representation). Depending on where the sensor is the image will be projected either on the sensor plane before or after the sensor. If we have it projected before or after the sensor we have a blurred object.
If we know the distances to the objeects, say 100cm, 1000cm, and 10,000cm (which are 10 times apart from each other) on the image it looks quite differently, because we don't have a linear conversion from the real world on the image plane (sensor, film, etc.), but it's more like a tangent function. In this case if we set the focal_length to 10mm we will have:
1/image = 1/10 - 1/object
Now for the 3 different object distances we have:
1/image = 1/10 - 1/100 = 90 / 1000, or image = 11.11cm
1/image = 1/10 - 1/1000 = 990 / 10000, or image = 10.1cm
1/image = 1/10 - 1/10000 = 9990 / 1000, or image = 10.01cm
If you take an object that is 100,000cm away, on the image it will be at 10,001cm
From this you can see that the closer the object the more prominent the projection position is, while with objects further away, the projections don't look that further apart. For that reason closer objects (on a wall that you look from the side) will look further apart while distant objects (at the end of the hallway) will look very distant at small focal lengths in comparison with the closer. But at the same time distant objects will look very close to each other. For this reason the objects in the middle that are in the distance look like they are vanishing quickly in the vanishing point than the objects that are closer.
And let me clarify once again: this perspective calculation doesn't have anything to do with barrel or other radial distortion. The radial distortion is changing the image on top of the perspective perception change.
This is why the perception of perspective is changed by the lens (contrary to your statement), but is not changed by the sensor.
Tihomir Lazarov , nope. Your basic statement " the wider lenses (without the radial distortion) will change the perception of distances between objects" is incorrect, and all following from that is incorrect.
The lens doesn't change perspective, the distance from the subject and other objects changes the perspective. If you do not change and of the distance relationships, but change only the lens, the perspective remains the same.
Put the widest lens available on your camera and take a shot without changing any distance relationships. Then mount successively longer lenses, taking more shots with each lens. You will find that angle of view is decreased, but perspective remains exactly the same.
In fact, if you crop the wide-angle lens to match the cropping of the longer lenses, you will have the same perspective matching each crop with each longer lens.
And you can go the other way by using a "long" lens on a larger format. Put a 100mm lens on an 8x10-inch camera, and the image will look "wide angle," but crop a 24x36mm rectangle out of that image, and the crop will look "long" again.
Changing the lens changes the field of view, not the perspective. Changing distance along with changing the lens changes the perspective.
The more correct term (that I used in the comment above) is "perception," not "perspective." It's squeezing pixels in the middle which changes the perception, not looking around the corner which is a change of the perspective. Objects will be again one behind the other, but pixels will be squeezed differently throughout the frame and thus perception for distances is changed. In the article I used the term "perspective" in combination with "to a certain extent," which wasn't technically correct although I clarified that I'm talking about objects distances in relation to each other, but here in the comment I used the right term: perception. I've never stated that you can see more of an object with one lens than with the other (when both objects are in the frame).
This is the reason why it's called "perspective distortion," which takes a perspective and distorts it working only with what is coming through the lens. The latter is constant, while the lenses are variable and thus the perspective distortion is different, but based on the same source objects (or source pixels if you will).
The perspective distortion will distort a flat image just like a filter in Photoshop. It won't change the objects in a 3D space but will squeeze or stretch "pixels."
You missed the point. There is no distortion, perceived or otherwise, changed by lens focal length.
The change is made by the distance relationship of the camera to subject.
What you don't take into an account is that this is not a camera obscura type of physics, but you have a series of convex and concave glasses which help see more than you could see with a camera obscura on the same sensor size.
In a camera obscura scenario (or a pinhole camera) you see more if you make your senso or your opening bigger. When your sensor area is small you can't project an object that is outside the field of view. With a lens that has a small focal distance (and relative to the sensor size we can call it a wide angle lens) you project the objects that are outside the field of view and thus it compresses the information. This makes the stretching of the image in a certain way that is expressed by the mathematical equasion I showed above. You can't escape that distortion (not talking about a radial distortion here) because you have non-flat lenses that work in an ensemble to make the objects project onto the sensor.
This is the reason interiors are not to be photographed with wide angle lenses regardless of the presence or abasence of radial distortion. Interiors must be shot with bigger sensors and normal lenses that don't distort the objects in order to fit them into the same sensor.
I'm attaching an image to show what a camera obscura would see (the top drawing) and why the sensor size is directly related to the field of view that will be projected onto the sensor. If you want to see more, you create a camera obscura with a bigger sensor because your "lens" is the same. But if you put a series of concave and convex lenses in front of the camera obscura opening in order to create a wide angle lens, you will get objects distorted (assuming no radial distortion is present).
You fail to see the flaw in that, very wide angle view, (yes, clearly exaggerated to demonstrate the effect, but you have an impossible scenario of a concave lens forming an image. That diagram does nothing much to illustrate the real world scenario.
Using a pin-hole camera, I basically reduced the lens to a “perfect, simple” lens. It gets rid of the formulas for CA, ED, etc., and makes things simple for our calculation. For a pin-hole camera to see the tree displayed, it merely needs the screen much closer, and much larger. That would be the equivalence of a wide-angled, simple, perfect lens.
In the real world, such a lens does not exists, which is why we get bokeh, CA, ED, etc., and have to consider rectilinear, stereoscopic, and curvilinear projections.
Still, you ore thinking in the box, and if you took these same diagrams and looked at the it from out of the box, you would see the simplification of the entire thing.
Perception of Distance
The perception of distance between objects in a 2-dimension photo is caused by the relative size of the objects. That is directly related to the ratio of the distances from the lens to the objects.
Your calculations are in the box for a 10mm lens, and is mostly irrelevant, because the position of the image relative to the film plane is not the deciding factor for the object size on the film. Think outside the box for a moment.
Using simple geometry, (no trigonometry required at all), taking similar objects you just did, one 1m away, one 10m away, one 100m away, and making them each 1m tall, then projecting them unto a flat screen through a pinhole, we see that the sizes of each object relative to each other is proportional to the distance each object is from the pinhole.
With the film plane 10mm from the pinhole, (10mm lens equivalence), or 100mm or 1,000mm from the pinhole, (100mm and 1,000 mm focal lengths equivalence), the relative sizes, ergo, the relative difference in apparent (perceived) closeness to each other, remains unchanged. This is true no matter the size of the screen the pinhole image is projected on. Replacing the pinhole with lenses, and the screen with film, does not alter the mathematics.
The triangles do not change, so the apparent sizes, hence the perceived distances, do not change. The only thing which changes the triangles, is moving the camera position, or moving the real distances between the objects.
Karim Hosein, I see that you voted me down… free to you to do it of course, but like this you just show how arrogant you are not accepting to be corrected when you say (write) something wrong. Any lens change the perception of distances between objects, it is just a fact of physics, and you can write all what you want I am sure that you will not change the laws of physics…
Any lens change the perception of distances between objects…
Of course you're right but some of us just shoot so practical inaccuracies are more beneficial than pedantic truths.
If all one does is just shoot, then the practical inaccuracies are neither harmful nor beneficial. That aside, I was referring to those trying to learn something to help them, not those who just shoot.
Help them in what way? Knowing certain lenses have certain effects should be enough. The whys and wherefores may be interesting but to what benefit?
«…certain lenses have certain effects….»
And there we go again. That sort of false information is not useful. Useful information is that perspective is a property of where one stands relative to the subject, and focal length sets FoV around that perspective.
There are examples of this misconception with long and short lens. First, two photographers standing in precisely the same spot, shooting planes in formation, one with a 200mm, the other with a 300mm, and the one with the longer lens, insisting that he will get better compression due to his longer lens. Second, two photographers shooting a house interior, one with a rectilinear fish-eye lens, the other with a “normal” lens, (focal length, 35mm, approximately equal to the image width, 36mm). The one with normal lens says that he takes several images and stitches them together, and because he is not using a fish-eye lens, he gets no “perspective distortion.”
Both of them are wrong. The photographer with the 250mm lens gets the same “distance compression” as the one with the 450mm lens, because they are shoting the same subject from the same place. The Photographer with the fish-eye lens and the one who is wasting time stitching together from the 35mm lens will get the same “perspective distortion” because they are shooting the same room from the same spot.
If they were taught that truth, that perspective was a matter of subject to camera position in space, then they would not be trying too hard to get an image which could be easier to do.
If one want s to talk about certain lenses have certain effects, talk about rectilinear projection lenses versus stereoscopic projection lenses. Those are certain effects which can be useful to know when taking certain pictures.
Well, then, good luck with that.
We're not talking about perspective changes here. Let me repeat that: it's a distortion just like getting an image in photoshop and applying a perspective transformation. In order to fit all the pixels in a frame the wide lens has to alter the image in some way and the simple calculations above show how each pixel finds its place. If you photograph something with two lenses (wide, 35 and longer, say 70) with objects that are close to you and are from both sides of the middle of the frame, you will see that the formula above is correct: the center parts of the image look quite similar with both lenses, because they are further away, but those that are closer to the frame and invisible for the "normal" lens (say a 50 on a 35 sensor) are much closer than those on the longer lens. If you crop out the sides of the frame, you are like looking through a longer lens, because that part of the optics that makes the different look is cropped out. And yes, first remove any radial distortion or shoot with a high quality wide angle lens that has minimized that.
Let me put it in a different way: If you want to see more of a scene: You watch something through a tube and you see a certain part of the environment. In order to see more of the scene you have to go back, but this will change the perspective entirely. For this purpose a number of lenses are made which are not a flat piece of glass, but with certain curvature that will allow you to project objects that are not normally visible through the tube into the same sensor size (the back opening of the tube). The objects that are straight ahead do not get much distortion, because they come straight through the glasses which can be almost assumed as "a flat piece of glass" in the center and there's not much bending. This is why when cropping the center of the image of a super wide angle lens, we don't see anything different from what we photograph with a super telephoto lens. The changes start to happen when we deviate from the center. Most high-end wide angle lenses try to keep straight lines straight, but as you have mentioned they distort other geometric shapes. This is what we compensate with for including more of the environment than we normally see through the tub without any lens.
«…just like getting an image in photoshop [sic] and applying a perspective transformation.»
«…to fit all the pixels in a frame the wide lens has to alter the image in some way….»
«…Most high-end wide angle lenses try to keep straight lines straight, but as you have mentioned they distort other geometric shapes. This is what we compensate with for including more of the environment….»
This is not a “Distortion” issue, but a “Projection” issue. It has little to do with the focal length, and more to do with the lens formula. This issue also occurs in tele lenses, but is only noticeable with a wide FoV.
Having said that. the issues of “edge distortions” which you bring up, although only noticeable with a wide FoV, hence, —by my definition of what constitutes a wide angle lens in another thread— only occurs in wide angled lenses. However, the nature of these edge distortions is not necessarily as you descried, as it depends on the projection of the lens one is using.
So going back to the statement, «One can't avoid the perspective perception change with a wider lens even without the radial distortion, because it's simply physics,» the answer is, “Yes one can, by simply choosing the correct projection, as the problem is not so much physics, as it is geometry.” The error with this is that, unless one has more than one wide lens, one has little choice but to fix in post, which ultimately means cropping the image.
«You watch something through a tube and you see a certain part of the environment. In order to see more of the scene you have to go back, but this will change the perspective entirely. For this purpose a number of lenses are made which are not a flat piece of glass, but with certain curvature that will allow you to project objects that are not normally visible through the tube into the same sensor size (the back opening of the tube).»
This analogy is that of the diagram you gave earlier, with the same fallacy, because other things change; the diameter of the tube, the length of the tube, and the distance of the tube from the sensor. This is one reason why Nikon et al are touting shorter flange distances; to make better wide angled lenses. On most SLRs, there is a limit to the minimum focal length lens available, and it is not a matter of projection, nor distortion, but a matter of the ‘length of the tube’. To accommodate this issue, lenses have been designed in the past which require the mirror to be locked up, so that they can set the elements of the lens further back in the camera.
Now when a camera has a flange distance of 45.46mm, —Pentax K-mount— the lens does need to do some pretty fancy stuff to allow a 10mmm lens —Pentax smc P-DA Fish-Eye 10-17mm ED (IF)— to focus to infinity. This fancy footwork does not prevent certain AoV or certain projection lenses, it just makes them more difficult to manufacture. The focal length (or AoV) of the lens does not cause the “edge distortion,” but the projection of the lens and the lens formula does.
«The changes start to happen when we deviate from the center.»
True with any projection. More true, when the AoV becomes greater, the effect of the projection becomes more pronounced, as we look towards the edges/corners. cartographers have had this issue for years. When mapping a 1 square kilometer piece of property near the equator, it really does not matter much, which projection they use. However, as they move towards the poles, or they start to map larger land masses, the projection of choice makes a big difference.
Which projection is correct? It really depends on for what purpose the map is needed. Same is true with photography and lenses. To wit, teaching, “One will get such-and-such ‘distortion’ when one uses a wide angled lens,” or “A wide angle lens always causes this-and-that ‘distortion’ at the edges,” is a fallacy which needs to be corrected, so that students of photography can stop having misunderstandings of [insert thing here] and stop avoiding them for [insert purpose here].
In this image, I used my raw processor of choice to somewhat alter the projection of choice, from the rectilinear projection of the 18-55mm lens, (at 18mm) to a more stereoscopic projection. This naturally resulted in a crop of sorts. It also made the horses legs appear a little “out of step” so to speak, but the rider's head no longer looks as weirdly elongated as the original. A different lens —such as the P-DA Fish-Eye 10-17mm ED (IF) at 17mm— may have given a better projection to start with, but I would not have been concerned with, “edge distortion due to the wide angle lens.”
«…others can have very successful and rewarding lives as photographers without the pedantry.»
I agree.
«…this level of specificity might muddle real world application of the concepts.»
I agree.
«Knowing the effect certain lenses weilds [sic] is enough for many to produce images of value.»
I agree.
My issue is when someone teaches them something which is incorrect, and the misunderstanding causes them to avoid [insert thing here] for [insert purpose here].
Certain lenses —such as rectilinear vs stereoscopic projection— do wield certain effects, and that knowledge is enough. “Wide angle lenses causes edge distortion which makes straight lines near the edges of the sensor appear curved,” is not one of those things.
"but any lens with an aperture of 25mm will have the same DoF"
That's just wrong.
It is precisely right. Doubt it? Try it any of the good DoF calculator apps available on iPhone, Android, or Internet.
Your saying it is wrong does not make it so, especially when physics and almost every DoF calculator app says that it is right.
Yeah, I doubt it because the actual optical formulas state that DOF is a function of CoC, focal length, focus distance, and aperture and that none of these factors affect each other linearly.
But maybe I interpret these wrong? Let's check with the help of the good old DOF calculator on www.dofsimulator.net:
CoC 0.03mm, Distance 500cm, constant diameter of the aperture 25mm.
50mm, f/2: DOF=1.21m
100mm, f/4: DOF=0.59m
Pretty dramatic difference right?
Maybe if we keep the framing constant?
50mm, f/2, 2.5m: DOF=0,30m
100mm, f/4, 5m: DOF=0.59m
Nope...
Saying "physics says that it is right" doesn't make physics say it's right.
Patience. I do not live on the Internet.
So, to clarify, I am speaking of a “"same image’ situation. I see that I did not make that clear in my last post, as I thought the context of the tread made it clear. On re-reading, maybe it was lost. Let me clarify what I was trying to get across.
When one considers out-of-the-box calculations, one is no longer considering “circles of confusions, but cones-of-confusions, from which these circles are derived. Likewise, we do not consider enlargement factors, because we are considering “perspective correct viewing distances.” It is because of out-of-the-box calculations, that lens manufacturers can place DoF scales on their lenses, as viewing distance and enlargement factors do not enter the equation.
My statement is based on achieving the same image —therefore same perspective, or distance— with different lens/sensor combinations, and both images enlarged to the same total width, and viewed from the same perspective corrected distance.
So, “they” say, that DoF is dependent on the ‘CoC’ —and they are probably referring to the “Circle of Confusion,” and not the “Cone of Confusion,”— the focal length, f, the focus distance, x, and aperture, —and by aperture, they probably mean the f-number— and you do not see how these are related? Okay, let us see how “they” did it.
At DoFSimulator dot net, they use the formula….. Wait…. Oh, they don't actually tell you. Well, that makes things difficult. …But we do know that, by looking at the DoF box, by, ‘CoC,’ they mean, ‘Circle of Confusion,’ introducing several rounding errors.
This means that their calculations must be based on sensor size, and enlargement size, and other factors (such as resolution), to figure out when a circle gets confusing. That already means that they are not using a ‘good DoF calculator,’ especially when they do not include viewing distance and enlargement factor. One can assume they are using the same final image size, say, 10×8 inches,* and the same viewing distance, say, 12 inches from the face,* but they don't actually say. They are therefore using in-the-box calculations. We can confirm this by simply changing the sensor size from 35mm to FT/MFT, and see the CoC reduced by a factor of 0.5.
*[These figures comes from the (alleged) “standard” enlargement size of 10×8 inch paper, and the 135 format frame which, when enlarged to a height of 8in, would fit 12in across, so viewed from 12in from the face. Other calculators use 25cm, which is about 10in from the face, (and a 10in width enlargement), to do the calculations. We do not know what DoFSimulator dot net uses.]
Secondly, from the lens box, we know that by, ‘aperture,’ they mean f-number. They also ask for focal length, and we know that the aperture —i.e., iris diameter— is dependent on the focal length, and the f-number, (or really, the f-number is dependent on the focal length and iris diameter). So already we have introduced approximations.
So, considering that this is NOT a good DoF calculator, let us do this again, at 5m, (a good portrait distance), and those two lenses, with aperture at approximately 25mm. Let us go with an f-type sensor, for the 100mm lens, and the MFT sensor, for the 50mm lens, so as to achieve the same enlargement amount, (different enlargement factors), to achieve the same image.
50mm @ f/2.0 gives DoF = 57.6cm
100mm @ f/4.0 gives DoF = 57.0cm
Oh, wow! Will you look at that? About a 10% difference only. Using a good DoF calculator, the DoF would be the same. But, to be sure, let us look at other DoF Calculators, and see if they can show us their formulas.
① DoF Master dot com.
There calculations ( http://www.dofmaster.com/equations.html) begin with calculating the hyperfocal distance, H. They then use that to calculate the minimum acceptable focus distance, Dn, and the maximum acceptable focus distance, Df.
Their Hyperfocal distance calculations shows dependence on the focal length, and the circle of confusion, but they do not state how they calculate the circle of confusion, only that it is dependent on the given CoC for the 35mm format size, (.030mm), and calculated for other sizes based on the “crop factor,” (a mostly useless term).
Since most places calculate the CoC for a 35mm format size based on an enlargement size of 10×8in, and viewed from a fixed distance of about 10-12 inches from the face, we see that they have simply ignored the perspective correct distance, and went with a fixed value. You and I both know that DoF is absolutely dependent on viewing distance and enlargement factor, so let us move on.
Their minimum acceptable focus distance is not only dependent on H, but also, once again, f, and the subject distance, s. (I use, x, but they use, s. I will stick with their variables here.) So now any errors involving, f, are increased proportionately, (not even considering the f²+f factor of the calculation of, H).
Their maximum acceptable focus distance in also similarly dependent on H, f, and s, increasing the errors in a similar fashion.
DoF is simply, Df-Dn, doubling the error again. To their credit, the f-number, N, is only used once (but in the calculation of, H, the top of the pyramid), and is calculated as actual powers of 2, and not the approximation used on most cameras/lenses.
Out-of-the-box calculations do not need the enlargement factor, film format size, nor viewing distance, because it uses the “Cone of Confusion” or the “Arc of Confusion,” which is what is used to calculate the cone of confusion in the first place. The arc of confusion, vertically, (or horizontally when using only one eye), is based entirely on the diameter of the pupil of the eye, and the radius of the eye. The first, for any given person, varies with light intensity, and they both vary from individual to individual. The value of 0.27' is taken from a mean radius and pupil size in an “adequately lit” room. (This is one of the many reasons why the lighting at galleries is carefully controlled).
Since the arc of confusion is what is used to calculate all the other factors except distance, and iris diameter, one can use the subject distance, s, to see that the subtended arc formed by two objects is only dependent on the distance away the two objects are, and the diameter of the iris.
I have to go now, but I will at some point later show a diagram, illustrating what I just said.
TL;DR →
To answer your question, “Did I make a mistake, or do you stand corrected?” The answer is, neither. I erred by not making myself clear. I hope this clarifies everything. If it does not, the diagram coming later will make it all clear.
Sure if you change sensor size you change the DOF. Since focal lenght is (roughly) reciprocal to the DOF and the cropfactor in a linear relationship doublling one and halving the other will result in roughly the same DOF.
May I remind you what claim you tried to refute?
The article is talking about how a wide angle lens will produce a deeper DOF than a classical portrait lens, not about how you can use the crop factor to calculate lens equivalencies across different camerasystems.
M43: 50mm @ f/2.0 gives DoF = 57.6cm
35mm: 100mm @ f/4.0 gives DoF = 57.0cm
You know what you could also prove with this scenario by applying the same logic?
M43: 50mm @ f/2.0 gives field of view (diagonal) = 24.4°
35mm: 100mm @ f/4.0 gives field of view (diagonal) = 24.4°
Therefore the focal length doesn't affect the field of view. Wait, what?
But by all means present the diagrams. Will be interesting.
I don't have a lot of time, but here is the first explanation of why we have the circle/cone of confusion. I will not go into the optics/physics in great detail, but when light (waves) pass through an iris, the waves at the circumference get diffracted, and as these waves hit the screen/sensor/retina, they cause diffraction patterns.
This first diagram shows the —very rough, not very accurate— depiction of two diffraction patterns of a point light source, one from a relatively wide iris, one from a relatively moderate iris. (Very interesting things happen as the aperture gets even smaller). As one can see, the smaller the aperture, (up to a degree), the better one can differentiate a large dot from a small dot. Our iris gets bigger in dim light, but smaller in bright light, which is why old, far-sighted, people like me can read better in bright light. We just cannot seem to focus in dim light.
The blue boxes depict the width of the smallest dot we can see. The point light source becomes a disc. Our ability to detect a point is more than simply dependent on our eyes' resolution. We “resolve” better in bright light.
Now take an “adequately illuminated room” and take the “average persons' eyes” at 20/20 vision, and we can calculate what size that dot will be. Better than calculating the size of the dot, (which varies by the eyeball size), we can calculate the arc subtended by the dot, on the average pupil diameter. (This is why optometrists first dilate your eyes, then put you in a dimly lit room, then ask you to read from a projected image of controlled brightness, or a chart with controlled illumination). By using the arc, we do not have to concern ourselves with the size of the eyeball.
That arc happens to be about a 0.027" arc. Once two dots are separated by an arc greater than that, the average person can differentiate them as two dots, (in an adequately lit room). Also note that some people have better than 20/20 vision. (X/Y vision means that one can see at X distance, what the average person can see at Y distance. 40/20 vision —and even better— is possible).
Now, just like optometrists do with their [EM3W] charts, we will do with photography.
If the arc (from our eyes) to two objects are greater than about 0.027", we can see two objects. If the “blur” of an out of focus object subtends an arc of less than 0.027", it still appears sharp. If two photographers look at an image, and one says the eyes are tack sharp, but the other says they are clearly out of focus, then one photographer simply has better vision. We are speaking here of the “average person.”
But to take it out of the box, we also have to deal with enlargement sizes and viewing distance. (Actually, even in the box, we must take this into account, and most DoF calculators do, but don't often tell you what criterion they use.). By using the “perspective correct viewing distance,” —the focal length of the lens, f, multiplied by the enlargement factor, E, Dp = f × E— we account for sensor size, enlargement, and viewing distance.*
So this is where the cone/arc of confusion comes from, which we will use for our out-of-the-box calculations/diagrams, later. I have to go, again, but hopefully, I will finish this tonight. (2018-10-31).
*(I can give diagrams for that, also, if you need that).
I really was hoping to get a reply, Karim. Did I make a mistake, or do you stand corrected?
Why is fixing something inherent to most non-stratospherically priced lens designs in post a bad idea? Not everyone has the need or ability to purchase ultra-high-level glass, and if the problem is inherent to the design, and you’ve the requisite sensor resolution to do so without adversely affecting the composition or output resolution, there’s no reason not to. Please show the level of respect the professional you clearly regard yourself as should show; there’s no need to patronize and call people names because their method isn’t what you would do. Constructive discussion is always welcome.
By the way, the crop sensor "fixes it in camera." by cropping out the most severe part of the radial distortion and leaving you less pixels. The full frame alllows you to use more of the area from the lens but if it has a severely visible radial distortion (e.g. barrel distortion) you need to fix it in post because this is what the lens physically delivers to your sensor and it has no other option, but store that in a raster file. What would you do next with the curved supposed straight lines you have to have? You fix them in post using either a software such as Lightroom, CaptureOne, or another, or use the Lens Correction filter in Photoshop. When you do such corrections it will crop pixels out, because it's a rectangular frame that you're bending pixels in.
And yes, software engineers in Adobe are making a living providing tools for correcting what manufacturers left so we don't have to pay big money for eliminating that defect. The same for software engineers at Phase One. We, as photographers are making a living by investing in the tools we think are best for your business. If you think it's better for your business to invest in crazy expensive non-radial distorting wide angle lenses, good for you. Others may invest in buying a piece of software and spend the rest of the money on a bigger camera sensor or something else.
Radial distortion is not the only issue at play. Even with a perfectly linear lens, wide angle projections can be visually objectionable. As one example, the linear projection of a sphere at the periphery of a wide angle view is an ellipse, not a perfect circle. While it's mathematically correct (see conic sections if you're a math nerd like me), that's not what our brain expects.
See my long comment above where it states exactly the same including some calculations. If we ignore the radial distortion we are dealing with optical physics here that depend on the focal length. This is what a real wide angle lens view is about. Most people don't like using wide lenses for portraits because of the radial distortion, not because of the so called perspective distortion (which is not changing the perspective, but distorting the existing perspective). But as the radial distortion is so prominent and dominating people ditch the wide angle lenses altogether. The article talks about (c) the radial distortion problem that turns people away from wide angle lenses most of the time. It's normal to have perspective distortion as shown in (b) in the diagram in the article which is the beauty of those types of lenses.
I haven't read all the comments, just gave them a quick view and they all sound interesting but I am curious to read what "wide" means, is wide 14mm (on a 35mm sensor), 20mm, 35mm...? Also, what is a portrait? I often read of "85mm for head shots" as well as "50mm for head and shoulders" or "35mm for environmental portrait" and so on, so I understand these are schemes and we don't have to follow them as well as composition restrictions bla bla bla but I while I find this article interesting being an amateur with a twist for portrait I'd like to see real life examples of "wide angle portraits" to try and understand if it could enrich my understanding of the hobby and open new frontiers.
Grazie for another interesting reading
A "normal" lens is considered the one that doesn't visually distort what you see with your eyes. A wide lens is the one that "sees more" than the normal lens (by making everything look further away in order to fit more pixels into the frame) and the long lens is the one that sees less than a normal lens and magnifying the portion of the area you want to see more.
All images in the article are shot with a wide-angle lens at the range of 24-35mm which is not super wide, but it's still wide for those who claim "85mm is for headshots."
It's quite interesting to shoot full-length portraits at 200mm and waist-up with a 24 or 35. If you keep the subjects away from the sides of the frame on the wide shots you won't see much of a difference the way how they look, but you will see quite a difference in the way the environment is changed through the optics.
I'm attaching an example where you can see the subject shot with a 25-30mm lens and with a 200mm one. I used the 200mm to make him look like he was jumping higher than he actually did. I just distorted the reality without photoshop because I had to do that "slam dunk" shot and as you see, I used 200mm for a full-length portrait.
The definitions vary, but a good rule of thumb is,
Superwide:
Approx f < W÷2
Wide:
W÷2 ≤ f < W
Normal:
W÷√2 ≤ f ≤ 2×W
Telephoto:
W×2 < f
Where;
W=width of the frame of the film/sensor format,
f=focal length of the lens
The whole idea of, ““normal” lens is considered the one that doesn't visually distort what you see with your eyes,” is non-sense, since, if viewed at the “perspective correct distance,” every print will not visually distort what one sees with their eyes.
‘Perspective correct distance’ is the enlargement factor × the focal length. That is, if the film is 24.5mm across, (APS-C, maybe), and the print is enlarged by a factor of 10, (to 245mm wide, or 10 inches, such as a typical 10×8 print), and the image was taken with a 50mm lens, then the perspective correct viewing distance is
50×10 = 500mm
(or about 20 inches from the face).
With a 200mm lens, the perspective correct distance for this image becomes 2m from the face, (about 6½ feet).
Again, simple geometry.
As for what focal length is “ideal” for portraits, the idea is to not cause obvious distortions in the apparent sizes of the different parts of the face, particularly, the nose relative to the ear. When one removes all outliers and considers the standard deviation of nose sizes to ear sizes, and the average distance from the nose to the ear, (again, removing outliers), then do the maths, one realises that the best minimum distance to stand to ensure that the apparent size difference falls within the standard deviation, becomes approximately 4m (about 13ft). (Beyond that distance, the relative sizes becomes more precise, but once it is within the standard deviation, our brains sees it as normal, or not distorted).
Once one is that distance away, (that is, one has set their perspective), one can then choose ones framing, that is, the focal length to attain the desired FoV. This will vary according to ones format size (and orientation).
That being said, sometimes deliberately exaggerating the apparent size of body parts may make for an appropriate portrait. The hand of a pianist, the nose of a perfumer, the legs of a dancer, etc.
I wasn't aware there was a misconception about using wide angles for portraiture? Sure, you're not going to use a 24mm for head shots, but i use a 35mm prime all the time for near head shot distances all the time.I'm glad i don't listen to anyone tell me what rules i need to follow for shooting (which would make for a more logical title to this article :)
Rules are a good thing, but there is a distinction between "good practices" and "rules," which is the case with portraits and lenses. A good practice shows long lenses look nice with headshots, but this is not a rule. Rules are a good thing.
Those images are a great use of a WA lens and a style I use frequently.
The REAL issue is the "traditional" head and shoulders portrait that makes the subject look like all nose.
Unless you shoot it more centered... which actually deviates from the "traditional." As I mentioned above, it's a good practice to use normal or long lenses for close-ups, but it's not a rule.
I use both prime and wide angle lenses for portraits. Although I am a bokeh fanatic and I lose some of that with a wide angle lens.
This could help someone. Wide/tele lenses just map part of sphere to the flat sensor. With the sphere far away from the sensor, curvature is smaller, so distortion is smaller - and vice versa. Objects on sensor axis are mapped almost directly, while on the edges they have to be transformed more.
Dashed line on the picture shows that telephoto lense is just mapping only "flat" plane.
So if I want prevent distortion - I should place subject as far as possible (with keeping my intent) and to the center as possible. Of course, that I can work with knowledge that our brain is benevolent toward some objects and their deformations (like bush) and more strict to other (like face)
Depends on the projection of the lens. If the lens has a rectilinear projection, then it tends to keep straight lines, straight, (but distorts circles). If it has a stereoscopic projection, then it tends to keep circles round, (but distorts straight lines by curving them). Then their is the curvilinear projection.
….And don't say, “Oh, you mean fish-eye!” No. Fish-eye is any lens which has a 180° AoV, regardless of its projection.
Also, most lens map a flat plane to a flat plane, so those curved lines you have would be somewhat wrong. This is why really good macro lenses are only really good at macro images. This is why older panorama cameras (with swing lenses), had curved film surfaces (as they were not capturing people in a straight line, but in a circle).
A wide angle is not a wide angle, is not a wide angle. All these generalisations of wide angled lenses are painting a false image —no pun intended— about shooting with wides.
Yup you mentioned it "it tends to keep". But with circles closer and angle wider it's so hard that most (if not all) lenses give up...
Just the cheap ones. Most actually do.
With Wide Angle you have to actually know what you are doing :D but it is much simpler getting an "instagram mom happy" picture of a highschool senior with a 200 f/2.8 ! There isn't much to mess up ! but with wide angle your camera angle is a lot less forgiving, the environment plays a huge rule and you have to have thought about it before clicking the shutter etc.. I love wide angle, still practicing to get better at it ...
Yes, the environment is very improtant with a wide lens. This is where if you shoot on sets every little detail matters especially if you want the eye to wander around only after being drawn to the main subject, not before that.
The reason wide angle is avoided for portraits is bc portraits are meant to showcase an individual. You typically try to remove as much of the surrounding environment as possible using blur or zoom. The idea of introducing extra real estate so one's eyes can wander has effectively ruined your portrait. In portrait photography your eyes are supposed to be attracted to the eyes of the subject, with any wandering of the eyes, being done over the subject.
Not to say it can't be done, or shouldn't be done. However, if you are trying to shoot a legit portrait, the 50mm rule isn't as important as the rule of isolating your subject from the background. These example shots are beautiful, but i wouldn't classify them as portraits.
Great article. To each their own. Its art, after all.