Every lens has a sweet spot, the aperture where the image sharpness is at its best. If the aperture becomes larger, lens errors will become visible. When the aperture is closed, lens diffraction will become visible. In this article, I am going to take a closer look at lens diffraction.
A small aperture increases the depth of field. It also improves lens performance. The lens will produce more overall sharpness. So, why don’t we use the smallest aperture as a standard? The reason is called diffraction. It is the interference of light waves that occurs when it travels through a small opening. It causes image sharpness degradation.
Light Waves and Small Openings
When light waves hit a barrier that contains an opening, that opening can be considered as a new point of origin. From that point, the waves will disperse.
A very simple visualization of light waves that travel through a small opening.
This can also be seen in the YouTube video I found, showing this effect in waves of water. Light is acting in a similar way.
But something strange happens. The light waves will show interference. In some places, these waves will be amplified, in other places, extinguished.
The corners of an opening can be considered as its own new point of origin, each producing its own waves. The drawings I made are projections on a flat surface. If you look at it in three dimensions, the light waves will show this interference when it hits the sensor. A point of light will be a spot surrounded by circles that decrease in sharpness and brightness with every next circle. This is called an Airy disk.
A large lens opening will make the Airy disk small.
If the lens opening becomes smaller, the Airy disk will grow larger.
Every opening will produce an Airy disk. But these will differ in size depending on the size of the opening. With a small opening, the airy disk will be larger and more pronounced. With a larger opening, the Airy disk is smaller and less pronounced.
The Effect of the Airy Disk on Your Image?
The size of the Airy disk depends on the aperture. A smaller aperture will produce a larger airy disk compared to a larger aperture. If the Airy disk is smaller than a pixel, it won’t be visible. The image will be sharp. When the Airy disk grows in size, it will eventually also cover the adjacent pixels. In that situation, the sharpness is decreased.
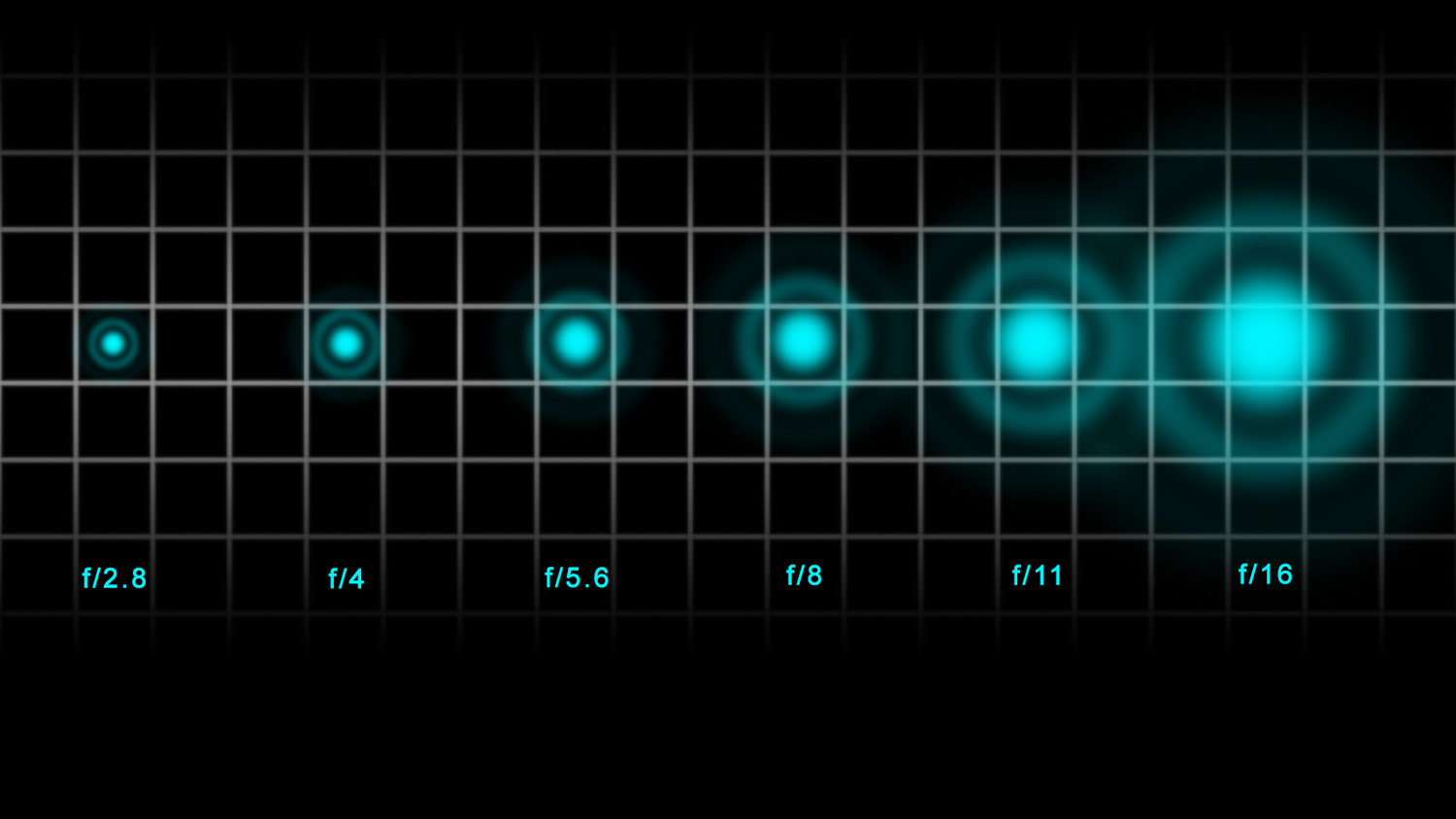
With a smaller lens opening, the Airy disk size increases. Just before the moment the Airy disk is larger than a pixel, the lens will likely have the best sharpness.
When the size of the Airy disk reaches the size of the pixel, the lens opening is considered the sweet spot. If this is an aperture of f/5.6, like in the drawing I made, the lens will produce its optimum sharpness at that aperture. The example image below was shot with a Canon EOS R5 and an RF 50mm f/1.2L lens. It clearly shows how a larger or smaller opening decreases image sharpness. At f/5.6, the optimal sharpness has been reached.
An example of lens performance on a Canon EOS R5 with different apertures. At f/5.6, the lens shows the best sharpness. This is the sweet spot of this lens.
The Effect of Sensor Resolution
Just before the Airy disk size exceeds the pixel size, the lens will perform at its best. In other words, the pixel size determines when diffraction becomes visible. A 50-megapixel sensor will show diffraction much sooner compared to a 25-megapixel sensor. To make it simple, the pixels of a 50-megapixel sensor will be half the size. An airy disk that will fall within the boundaries of the pixels on a 25-megapixel sensor will cover more pixels on the 50-megapixel sensor.
Smaller pixels will show an Airy disk much sooner.
The Effect of Sensor Size
The size of the Airy disk is only determined by the lens opening. The sensor size has no effect on the Airy disk size that belongs to a certain lens opening. If the amount of pixels per square inch is the same between, let’s say a full frame sensor and a 1.6 crop sensor, the diffraction will be exactly the same.
Although the Airy disk is the same, it looks larger on a smaller sensor. If the amount of pixels per square inch is the same, the diffraction will be the same. But the Airy disk will be visible much sooner if both sensors have the same amount of pixels.
In other words, a 25-megapixel full frame sensor has approximately the same amount of pixels per square inch as a 16-megapixel 1.6x crop sensor because the amount of pixels per square inch is roughly the same. But if the crop sensor also has 25 megapixels, the number of pixels per square inch is increased. In that case, diffraction will be visible much sooner.
The Effect of Focal Length
With focal length, it becomes more complex. For that, we first need to know how the lens opening is affected by the focal length. After all, f/8 on a 50mm lens will be the same as f/8 on a 100mm lens when it comes down to exposure.
In reality, the physical lens opening depends on the focal length. The real lens opening of a 50mm lens and f/8 is 50/8 = 6.25mm. With a 100mm lens, the real lens opening is only 100/8 = 12.5mm. Thus, a lens opening of f/8 will become larger when the focal length increases.
Still, the amount of light that hits the sensor will be the same regardless of the real physical lens opening. This is because of the focal length itself. With 100mm focal length, the light needs to travel twice as far compared to a 50mm focal length. After all, the focal length is longer. Because the distance is twice as long, the amount of light that reaches the sensor is half as much. It's a bit more complex than this, but you get the point by this simplified example.
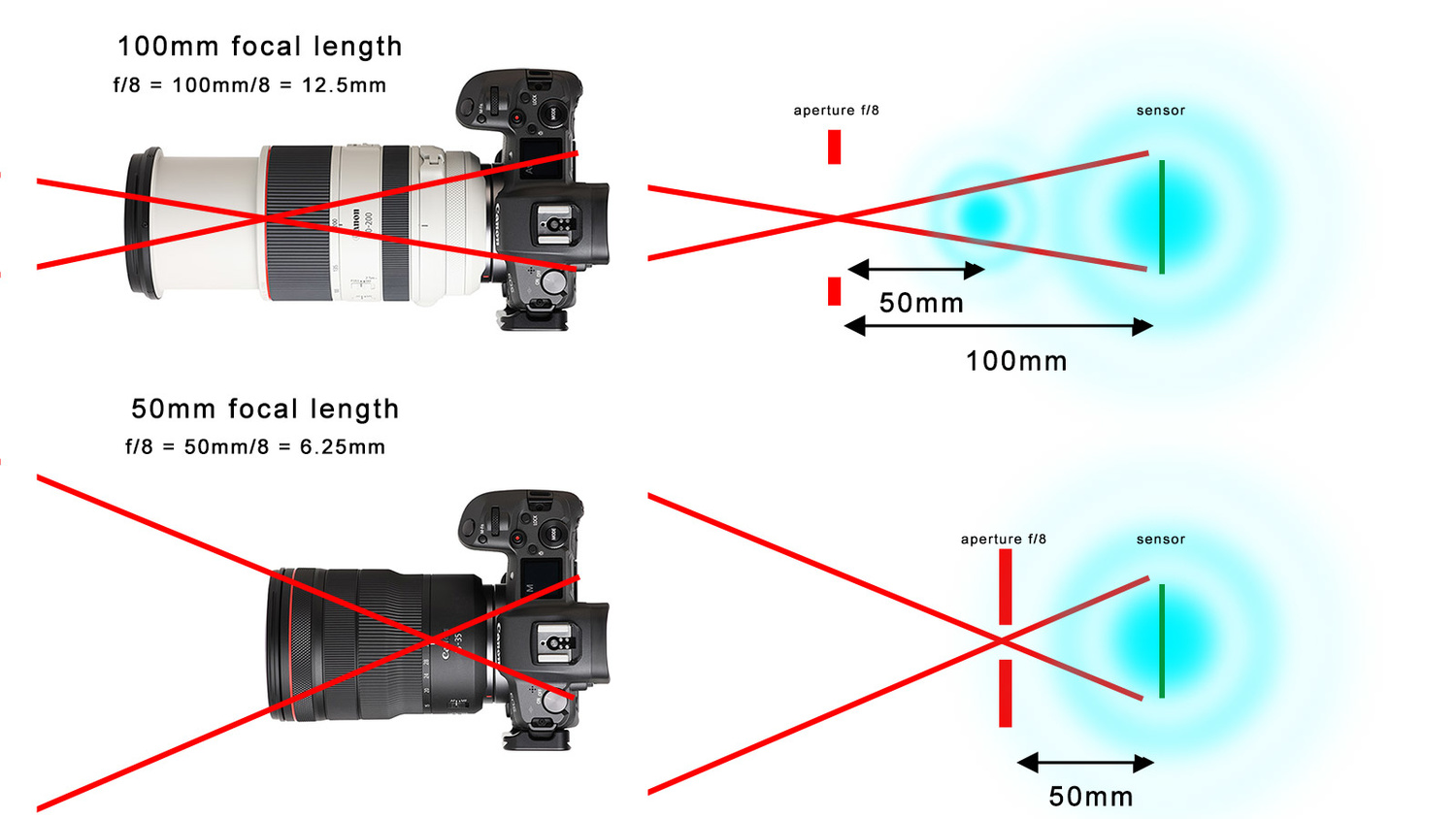
Although the lens opening with a certain aperture is larger with longer focal length, the magnification will also increase the airy disk
Now, we have seen how a larger lens opening will decrease the size of the Airy disk. The larger physical lens opening of f/8 with 100mm is producing a smaller Airy disk compared to a 50mm and f/8. But the Airy disk is the projection of the light on the sensor. With a longer focal length, the light needs to travel twice as long before it reaches the sensor, thus magnifying the Airy disk by a factor of two.
Although the Airy disk with an increased focal length will produce a smaller Airy disk, you need to take the magnification factor of the focal length into account. This will cancel each other out. The result will be approximately the same Airy disk size with a certain aperture, regardless of which focal length you are using.
Image Resolution Determines the Amount of Diffraction
Diffraction is always occurring. But the lens opening or aperture is determining how strong the diffraction will be. When the Airy disk becomes larger than a single pixel, diffraction will become visible.
Although the real physical lens opening with a certain aperture depends on the focal length, the magnification of the lens will counteract the smaller Airy disk. This means focal length will have no visible effect on the amount of diffraction.
The only thing that will have an effect on the amount of visible diffraction is resolution. More pixels will make the Airy disk become visible much sooner.
Nando,
This is a very nice and clear description of diffraction. But I think you have a small error with your math. I always enjoy your articles and laud your attention to detail, so I thought you might appreciate a little feedback.
You state that a 16 MP, 1.6 crop has the same pixels per area as a 25 MP. I think it should be 10 MP, 1.6 crop. The pixels per unit area scale with the square of the crop factor. You also state that the pixels on a 50 MP sensor will be half the size of a 25 MP sensor. They will be half the area, but 0.7x dimension per side, which is more relevant to the imaging of the Airy disk, since the diameter of the Airy disk (not the area) is function of f-number. So your diagram is a little erroneous because it looks like the 25 MP sensor pixel is twice the length of the 50 MP pixel.
These are just nits and don't really diminish your article, but some readers might be a little confused if they try to get their math to match yours.
Hope this helps. Keep the articles coming.
Thank you for your comments and corrections. Appreciate it.
Although the dimensions and sizes may not be spot on, the principle stays the same.Fortunately ;)
Nando, I think this is not correct, even not correct at all (light intensity would decrease by 1/sqr(r) while r is the distance to the light source. But that is not valid for a lens which projects to an image circle which of course is at least just a bit bigger than the sensor.
"With 100mm focal length, the light needs to travel twice as far compared to a 50mm focal length. After all, the focal length is longer. Because the distance is twice as long, the amount of light that reaches the sensor is half as much."
Diffraction does not depend on the f-stop but on the aperture (k = f / D) (f = focal length, D = diameter). So I'd skip all the text about f-stop. It is just confusing.
I may misunderstand this "More pixels will make the Airy disk become visible much sooner." But the airy disk is there and has the same size regardless of the number of pixel on the sensor. What it should say is: With more pixels you get a better resolution but the diffraction will soften your image. So the more pixels a sensor has, the wider the aperture must be to take advantage of the high resolution of a sensor.
With a 1.5 crop factor 36MP FX (full frame) is about 16MP DX (cropped sensor). I think this all should be corrected.
"With 100mm focal length, the light needs to travel twice as far compared to a 50mm focal length. After all, the focal length is longer. Because the distance is twice as long, the amount of light that reaches the sensor is half as much."
No, the amount of light reaches the sensor is only a quarter, because the image is twice as big by side but is four times big by area. The same thing with flash to subject distance: when you double the distance you lose two stops, that is four times the amount of light.
That's correct.
I keep on thinking about size by side and not the surface area...
Hello, why the most open aperture have the shortest depth of field? Everywhere i read that closer aperture causes Airy disc. And Airy disc causes more blurry pixels. But opposite is true, the closer aperture have less blurry pixels and longer depth of field.
Lens diffraction is caused by the Airy disk size. Depth of field on the other hand, is the result of the Circle of Confusion. Those are two different things.