A Practical Guide to How the Inverse Square Law Affects Your Subjects and Background

I don't care what anyone says. Math and physics are cool. Nonetheless, I understand that you don't particularly need all the theory when you're lighting a subject; you just need to understand how to get the result you want. These helpful videos will show you just that.

Coming to you from Pixel Viilage, these two videos will explain how the inverse square law affects the lighting of multiple subjects and the lighting between a subject and background. Remember, the inverse square law states that for every time you double the distance of the light source, the intensity of the light on the subject becomes one quarter as strong. Why is this? The light now has to cover quadruple the surface area. And while that's important, you also need to consider the idea of the relative distance vs. absolute distance. Watch the two videos below to see it in practice.

Multiple Subjects

Subject and Background

So, what's really going on here? We're seeing how the relative distance is more important than the absolute distance in practice. For example, consider the two scenarios below:

• Light is one foot from the subject and subject is one foot from the background. Light is set to properly expose subject.
• Light is eight feet from the subject and subject is one foot from the background. Light is set to properly expose subject.

The distance between the subject and background doesn't change, yet we can expect the background to be relatively dark in the first example and almost the same exposure as the subject in the second. Why is this? That's because relative to the light, the background is twice as far away, and since the intensity ratio is the ratio of the squares of the distances, we can expect the light intensity on the background to be:

As expected, the background receives a quarter of the light. On the other hand, in the second scenario, while the absolute distance hasn't changed, the subject and background are much closer relative to the overall distance of nine feet across the entire setup. This is reflected in the inverse square law for this scenario:

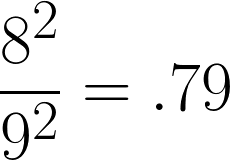Despite the subject being the same distance from the background, the background receives a little over three quarters the light the subject does, much more than the first scenario. This is why photographers often need a light on the backdrop when they use a modifier up close. Understanding these relationships will make your lighting work much easier when working with multiple models or a background.

[via Pixel Viilage]